by Frank Hellman, Albert Einstein Institute, Golm, Germany
Jacek Puchta, University of Warszaw
Title: The Feynman diagramatics for the spin foam models
PDF of the talk (3MB)
Audio [.wav 35MB], Audio [.aif 3MB].
In several previous blog posts (e.g. here) the spin foam approach to quantum gravity dynamics was introduced. To briefly summarize, this approach describes the evolution of a spin-network via a
2-dimensional surface that we can think of as representing how the network changes through time.
While this picture is intuitively compelling, at the technical level there have always been differences of opinions on what type of 2-dimensional surfaces should occur in this evolution. This question is particularly critical once we start trying to sum over all different type of surfaces. The original proposal for this 2-dimensional surface approach was due to Ooguri, who allowed only a very restricted set of surfaces, namely those called "dual to triangulations of manifolds".
A triangulation is a decomposition of a manifold into simplices. The simplices in successive dimensions are obtained by adding a point and "filling in". The 0-dimensional simplex is just a single point. For the 1-dimensional simplex we add a second point and fill in the line between them. For 2-dimensions we add a third point, fill in the space between the line and the third point, and obtain a triangle. In 3-d we get a tetrahedron, and in 4-d what is called a 4-simplex.
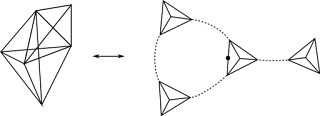
The surface "dual to a triangulation" is obtained by putting a vertex in the middle of the highest dimensional simplex, then connecting these by an edge for every simplex one dimension lower, and to fill in surfaces for every simplex two dimensions lower. An example for the case where the highest dimensional simplex is a triangle is given in the figure, there the vertex abc is in the middle of the triangle ABC, and connected by the dashed lines indicating edges, to the neighboring vertices.
All current spin foam models were created with such triangulations in mind. In fact many of the crucial results of the spin foam approach rely explicitly on this feature rather technical point.
The price we pay for restricting ourselves to such surfaces is that we do not address the dynamics of the full Loop Quantum Gravity Hilbert space. The spin networks we evolve will always be 4-valent, that is, there are always four links coming into every node, whereas in the LQG Hilbert space we have spin-networks of arbitrary valence. Another issue is that we might wish to study the dynamics of the model using the simplest surfaces first to get a feeling for what to expect from the theory, and for some interesting examples, like spin foam cosmology, the triangulation based surfaces are immediately quite complicated.
The group of Jerzy Lewandowski therefore suggested to generalize the amplitudes considered so far to fairly arbitrary surfaces, and gave a method for constructing the spin foam models, considered before in the triangulation context only, on these arbitrary surfaces. This patches one of the holes between the LQG kinematics and the spin foam dynamics. The price is that many of the geometricity results from before no longer hold.
Furthermore it now becomes necessary to effectively handle these general surfaces. A priori a lot of those exist, and it can be very hard to imagine them. In fact the early work on spin foam cosmology overlooked a large number of surfaces that potentially contribute to the amplitude. The work Jacek Puchta presented in this talk solves this issue very elegantly by developing a simple diagrammatic language that allows us to very easily work with these surfaces without having to imagine them.
This is done by describing every node in the amplitude through a network, and then giving additional information that allows us to reconstruct a surface from these networks. Without going into the full details, consider a picture like in the next figure. The solid lines on the right hand side are the networks we consider, the dashed lines are additional data. Each node of the solid lines represents a triangle, every solid line is two triangles glued along an edge, and every dashed line is two triangles glued face to face. Following this prescription we obtain the triangulation on the left. While the triangulation generated by this prescription can be tricky to visualize in general, it is easy to work directly with the networks of dashed and solid lines. Furthermore we don't need to restrict ourselves to networks that generate triangulations anymore but can consider much more general cases.
This language has a number of very interesting features. First of all these networks immediately give us the spin-networks we need to evaluate to obtain the spin foam amplitude of the surface reconstructed from them.
Furthermore it is very easy to read off what the boundary spin network of a particular surface is. As a strong demonstration of how this language simplifies thinking about surfaces, he demonstrated how all surfaces relevant for the spin foam cosmology context, which were long overlooked, are easily seen and enumerated using the new language.
The challenge ahead is to understand whether the results obtained in the simplicial setting can be translated into the more general setting at hand. For the geometricity results this looks very challenging. But in any case, the new language looks like it is going to be an indispensable tool for studying spin foams going forward, and for clarifying the link between the canonical LQG approach and the covariant spin foams.
Monday, October 31, 2011
Subscribe to:
Post Comments (Atom)



No comments:
Post a Comment